評価すること

院試向けに微積分の復習をしています.
Stirling's approximation(スターリングの公式)

は,n!を近似で評価しようというものです.
階乗はnがそれほど大きくなくてもすぐ発散してしまうので
計算が難しいです.ですから
比較的手に追える式に落としこんで評価することが
できると嬉しいことが多い…ﾊｽﾞﾃﾞｽ.
スターリングの公式の肝は,
logxという関数の積分の評価です.
ざっくりと天下り式な証明を紹介します.
スターリングの公式を導くにはウォリスの公式を使う形に
なんとしても持っていくという方針に従えば
証明を見失うことはないと思います.
天下り的に次の数列の評価を行います

この数列は(n!)をn^(n+1/2)*e^(-n)で評価することを考えて出てきます.
この時,

であり,

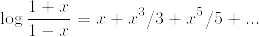
を利用してやると,

を得ます.
ここで更に二つの数列a_n,b_nを次のように定義してやります.

a_n < b_n
であり,
d_n -d_(n+1)の不等式評価より,
a_1 < a_2 < a_3 < ... < a_n < ... < b_n < ... < b_1
を得る.
ここで,
b_n = a_n * exp(1/12n)なので
b_n - a_n -> 0(n -> 0)である.
よってカントールの公理より二つの数列は収束することになる.
ここで,a_n,b_nの収束性より0<θ<1となるθを用いて

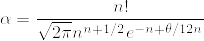
と表せる.
ここまで来たらウォリスの公式

にαの式を代入してやって,
α=1を得る.
ゆえに,b_nの収束値がαであることから,
スターリングの公式を得る.
うはぁ…結構厳しいのね.

確率論ではそこそこ使われたりするので覚えておいて損はないかも…

ちなみにこの評価の相対誤差は,
(1-exp(-1/12n))です.(上の評価式から直ちに導けます.)