2010/3/15の日記の転載:Brachistochrone curve

つい先日お台場にあるPanasonicセンター東京内のRisuPiaに行った際に,
「決まった二点間で曲線に沿ってものを落とした時に
最下点まで一番早く到達する曲線は何か？」
という問題に出くわしました.
答えはあまりなじみのない曲線に行きつくのですが,
変分法を用いて導き出すことができます。
便宜上二点間をA(0,0)B(x,y)ただしy>0と置く.
xの関数yの汎関数I[y]が極値を取る場合に
オイラー・ラグランジュ方程式を満たすことを思い出します.
この場合の汎関数はAからBまでかかる時間として、
時間がs(曲線の長さ)/v(速度)を積分したもので与えらるので,

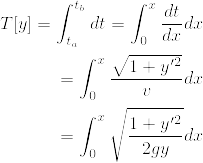
と表わされます.
ここでv(x,y)はエネルギー保存則よりyの関数として与えられます.
この積分の中のFをオイラー・ラグランジュ方程式に代入して解いていきます.
Fがxに陽に依存しないために,
オイラー・ラグランジュ方程式は簡単になって,次のように解けます.
上の式の前半はベルトラミの定理というもので,
Fがxに陽に依存しない場合に
オイラー・ラグランジュ方程式が簡単になるので比較的有効な手段です.
下の微分方程式を満たす曲線が求めるべき曲線ですが,
これはサイクロイドと呼ばれる曲線の満たす微分方程式となります.
サイクロイドは媒介変数で表わされる曲線で,θを媒介変数とすると,
という風に表わせます.
この曲線が最速降下曲線となるのですが,
実はサイクロイドには面白い性質があり,
どこから落としても最下点に辿り着く時間は一定となります.
東京大阪間がだいたい400kmとして,
一番初めのT[y]の式を解くと,

ここでAは定数で2Aπ=xで
東京大阪間に摩擦の無いサイクロイド型のトンネルを作ったならば,
約500秒(8.3分)で東京まで着くことになります.
この時最下点での物体の速度はエネルギー保存則より
約1.6[km/s]ということになり,
海面上で気温15℃の時に音速が340[m/s]なので
音速の4倍以上ということになります.
もともと上記の問題は
手元のE.ハイラー/G.ヴェンナーの[解析教程]

解析教程〈上〉

によると
ヨハン・ベルヌーイがコンテストとして公に提示した問題で、
締め切りまでには多数の解答が寄せられたそうですが,
自らの解答が最もエレガントだったそうです.
その方法はフェルマーの原理のアナロジーを利用するというものでした。
それは速さが物体の速さがv=sqrt(2gy)で与えられるような層を
いくつも考えるというものでした.
ところで、このヨハン・ベルヌーイという人は
天下のベルヌーイ一族の中でもくせものだったらしく,
微分についてのニュートンVSライプニッツ論争が起こっている際には
率先してライプニッツに加担したり,
兄のヤコブ・ベルヌーイとは常に衝突ばかり.
挙句の果てには息子のダニエル・ベルヌーイの業績を盗もうとしたとか.
もちろん何が真実で何が嘘なのかは今となっては分かりませんが,
天才にはスキャンダルやルーマーはつきものですね。
ところで,抵抗・摩擦を含めた際の最速降下曲線はどんな形になるのでしょうか？
気になるところですね.